Generalised geometry #9: Generalised diffeomorphisms and double field theory

Generalised geometry: A study of generalised diffeomorphisms and gauge transformations

We finally arrive at one of the most important properties exhibited by generalised geometry: namely, the manner in how generalised structures preserve a change of to . As discussed in the previously, this means that we have a pairing of linear transformations that become orthogonal transformations. We also reviewed in a past note about how the Lie algebra of sections of becomes the Courant algebroid . But what about diffeomorphisms? From a physical point of view, this is one of the most interesting questions that we can ask; indeed, the study of generalised diffeomorphisms has been an implicit motivation from the outset.

In studying diffeomorphisms in the generalised geometric context, let it be clear that we are interested in diffeomorphisms of that therefore preserve the structure of . The notion of a generalised diffeomorphism will be entirely analogous to later considerations in the context of double field theory geometry. In principle, and looking ahead, this means that such a map must act on any given fibre as a linear map to another fibre: i.e., underlying this structure is the diffeomorphisms of the smooth manifold .

But let’s not get too abstract too soon. The main point for now is that there are a number of approaches to probing the structure of generalised diffeomorphisms and gauge transformations. We shall start with a study of bundle endomorphisms. Considering again the structure group generators in [LINK], equipped with these tools and those analysed throughout the last few notes, we will first look at what transformations in valued algebra leave the inner product invariant and the Courant bracket unchanged.

From endomorphisms to bundle endomorphisms

Recall from a past discussion the study of the generalised vector space , from which we moved to consider the notion of a generalised tangent bundle such that with a smooth manifold. The symmetry transformations in Note 3 apply in this context, where we found that the linear endomorphisms of that preserve the bilinear form is the orthogonal group . In the more general case, these endomorphisms become bundle endomorphisms. These bundle endomorphisms are sections of . In making this generalisation, the B-transform involves a section of , i.e. a two-form. While continuing to preserve the bilinear form, as we’ll see this B-transformation becomes especially important (indeed, another stringy hint resides here).

As an initial step, consider the statement that any transformation in leaves the inner product invariant. Consider, for example, a B-shift (Note 3 linked above) with two generalised vectors . The exponentiation of the antisymmetric transformation (again, see Note 3) can be written as

and we see that

where we use the antisymmetry of the inner product when contracted with the 2-form such that .

As the whole transformation group leaves the inner product invariant, in order to find the exact subgroup that preserves the general Courant structure we have to look at the transformation of the Courant bracket. It is already somewhat obvious that the Courant bracket is invariant under diffeomorphisms, given it is defined by a coordinate-free expression. But, unlike the Lie bracket, it has an important additional symmetry: it is preserved under B-field transformations, which are B-transforms with the demand that B is closed.

To see this we note that we shall make use of the Cartan identity

which implies . And so we now we want to apply a B-shift to the two sections of the generalised bundle , take their Courant bracket and substitute the form in eqn. 4 of Note 4.

Proposition 1 (The two-form must be closed) The transformation is an automorphism of the Courant bracket if and only if is closed, i.e. . Let and be two sections of , and define as a two form. Then

Proof: We begin the proof similar to (1):

where we see that is an automorphism of the Courant bracket if and only if for all . Hence, the requirement .

Courant automorphisms

To understand the symmetries of the Courant bracket, we need to understand its automorphisms. Recall that an automorphism is an isomorphism from a mathematical object to itself preserving all of that object’s structure. The set of all automorphisms of an object forms a group, namely the automorphism group.

An orthogonal Courant automorphism is defined by the pair with denoting diffeomorphisms of and of such that represents an orthogonal linear map on each fibre of . This means that satisfies . Combined with the operation of composition, the group of orthogonal Courant automorphisms of is defined.

Define the diffeomorphism of , then smooth sections of transform as

The pair is therefore an orthogonal Courant automorphism. It follows that a subgroup of Courant automorphisms can then be written

But we may also define the subgroup

which now allows us to show that every orthogonal Courant automorphism can be made from a diffeomorphism and a B-field transformation.

Group of generalised diffeomorphisms

As we saw, given the Courant bracket possesses an additional symmetry when compared with the standard Lie bracket – namely, invariance under B-field transformations – an important observation can now be made. The full group that simultaneously preserves the Courant bracket and the inner product is the group of diffeomorphisms on the manifold that we may denote as .

Theorem 2 (Group of generalised diffeomorphisms) Courant automorphisms, which preserve all of the structure of the generalised tangent bundle , are a composition of diffeomorphisms and B-field transformations. The generalised diffeomorphism group is

where denotes the set of closed 2-form fields on . It can also be proven that this is the only group that preserves this structure.

Proof: For covering , consider the map , where is defined below in (13). Since covers the identity (by definition), we may apply the Leibniz rule for

= G([X,Y]),

to obtain the projection . This means that necessarily has the form

By orthogonality we obtain such that . Thus , and from before it also follows must be closed.

Any generalised diffeomorphism can be written as where and .

For we have semi-direct product structure of the form

where the action on is by pullback.

Several remarks are now in order. When extending the analysis from ordinary geometry, which considers the tangent bundle with the Lie bracket, to generalized geometry, which considers exact Courant algebroids with a Courant bracket, it is clear from what we have reviewed that we are considering an enlarged group of symmetries in which diffeomorphisms are a subgroup.

In the semi-direct product (7) different transformations are therefore encoded. Diffeomorphisms take a point in the manifold and map it to another point. So diffeomorphisms are transformations on the manifold. B-transformations, or B-shifts, are local transformations acting on the fibre elements leaving the point on the manifold fixed. Hence, these transformations are pointwise.

Finally, note that for the case where it is possible to define the -twisted version of the Courant bracket, where is the familiar closed three-form. The Courant bracket then takes the form

Under a B-transform this bracket satisfies

Generalised diffeomorphisms

We arrive at the punchline. Let’s now look at the concept of generalised diffeomorphisms from a physics bias, emphasising particularly the structure of the Jacobians.

Consider first the standard case. For any diffeomorphism that is a bundle map, the transformation induces a diffeomorphism . This is true if we replace with any vector bundle.

For the standard case where the group of diffeomorphisms are bundle maps, the action is linear and satisfies

such that we have exactly the differentials of diffeomorphisms . Proof of this statement is fairly straightforward. For the conventional Lie bracket invariance under a pushforward can be represented by a commutative diagram

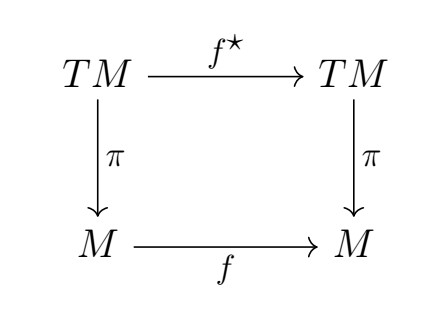
with a diffeomorphism and the pushforward on the tangent space to at the point . As is a diffeomorphism it follows acts on a vector field such that .

The commutative diagram states that the Lie bracket commutes with the pushforward action that is precisely the statement (10).

We now want to extend this analysis to the generalised case.

Definition 3 (Generalised diffeomorphisms) A generalised diffeomorphism is a bundle map that preserves the pairing and satisfies

for all .

This means that for a diffeomorphisms , with the Jacobian and its inverse, the orthogonal bundle map

is an example of a generalised diffeomorphism.

As a brief remark, note that we define the pullback of a form field as , and so we may also define the map as . Now we may observe that the Courant bracket commutes in direct analogy of the Lie derivative. So in (12) we have .

The following commutation diagram describes the generalised case:

Crossing the bridge to physics

We have reached the point in our review of generalised geometry that we can now cross the bridge and think about physics. As we have discussed through the course of several notes, in generalised geometry the geometric objects defined on a tangent bundle (or cotangent bundle) of a manifold are instead defined on the generalised bundle . This geometry, we will see, has proven to have a very close relationship with the geometry of string theory, especially through the 2-form b-field and the workings of T-duality, but also Dp-branes, topological strings, and the study of flux compactifications. This geometry naturally accommodates , an indefinite metric of signature , a positive-definite metric that combines and , among other notable results.

In particular, we will realise this connection through what is known as double field theory. The doubled geometry of double field theory is also motivated by a fundamental duality of string theory (T-duality), but it starts from the idea that the dimensionality of the manifold itself should be doubled (as we’ll discuss, this comes from the use of doubled coordinates ). Although many questions remain about the nature of doubled geometry, in a few of the well-known approaches and proposals the resulting space is assumed to have an indefinite metric, again of signature , which breaks the expected structure to the T-duality group . In many ways, we will see why there is good argument for how double field theory geometry extends beyond generalised geometry in the sense that it includes generalised geometry, which is to say it is more general. What that means, precisely and with sound definition, is a topic of ongoing research. We will discuss some of the leading hypotheses.

An important focus moving forward, as we transition to a series of notes on double field theory and its geometry, will concern in what ways the notion of generalised diffeomorphisms relates with the physics of doubled diffeomorphisms. In particular, we will take all of the insights extracted from a review of the essential structures of generalised geometry and apply them to a study of doubled geometry – that is, the geometry of manifestly T-duality invariant string theory. One of the very first observations we will make will prove very neat: the NS-NS supergravity fields and transform under diffeomorphisms and two-form abelian gauge transformation such that, when combined, the field content will be written precisely to ensure invariance. This is the exact same sort of structure we have already been discussing. Indeed, the usual gauge transformations of the metric and b-field will be lifted to -covariant gauge transformations of the generalised metric (an object we naturally introduced in a past note) and the dilaton . In connecting with the physics of string theory, we will also see how the Courant bracket and many other generalised objects appear. Toward the end, we will then discuss another open research topic concerning doubled geometry on the string worldsheet.

In the very least, this is a loose sketch of some of what is to come.

Generalised geometry #8: Complex and symplectic structures

Before moving on to the important topic of generalised diffeomorphisms, not much has been said yet about extensions to complex geometry. As a short note, it is worth mentioning a few details as generalised complex structures are a primary subject of study in the context of the generalised geometry programme. These are structures on that extend the definitions of complex and symplectic geometry, with generalised complex manifolds having integer entries at each point, called a type, according to which symplectic manifolds are type 0.

Consider again the linear theory with a vector space. We can introduce a complex structure on such that there is an endomorphism satisfying . To introduce a symplectic structure on , we can define a linear homomorphism such that is skew-symmetric and non-degenerate (and so is invertible).

Both of these structures can be generalised according to the following definition.

Definition 1 Let be a vector space. A linear generalised complex structure is a linear homomorphism such that

1. J is a complex structure ,

2. J is skew-adjoint ,

where is the natural bilinear form on .

It then follows that a complex structure defines a generalised complex structure

where denotes the dual map .

A symplectic structure defines a generalised complex structure of the form

It then follows that we can expand from these definitions of generalised complex structures to study to maximal isotropics, spinors, generalised almost complex structures, topology, integrability, and finally generalised Calabi-Yau manifolds.

Generalised geometry #7: Generalised metric

Generalised metrics and generalised Riemannian geometry

We can introduce further structures on the generalised bundle leading to further geometries. The first is the natural metric on . The second is a generalisation of the Riemannian metric and is therefore called the generalised metric. Upon introducing this object, it follows we may also extend other familiar objects such as a generalised Levi-Civita connection, Hodge star product, and so on (although we don’t study the derivations of these objects in these notes). In many ways, it is possible to directly motivate the notion of extended Riemannian geometry or what is sometimes also called generalised Riemannian geometry, through its close connection to generalised geometry.

O(d,d) constant metric

Defining a metric on a generalised space is equivalent to how a group is a structure on a set. Given the non-degenerate inner product with signature , then for some 2D-dimensional vector (See eqn. (28) in note 3) we can directly express the metric

with

where . After diagonalisation we find

This metric can be seen as the invariant tensor of a group of matrices, namely . In other words, as is the constant metric, it serves to reduce the structure group of the bundle to .

The transformations that leave this inner product (1) invariant are transformations such that is the property of split orthogonal matrices. (There is no restriction on the vector fields being integers and hence they take values in ).

Remark 1 (Further comments and intuition about ) In fact, as we have seen in the proceeding analysis, the naturally arises from the linear structure of the generalised tangent bundle . And as we observed in a study o the structure group generators (again, note 3 linked above), the structure group is that acts on the , which is in direct analogy to how, in the standard geometry, acts on the fibres . From a geometric perspective, this viewpoint gives further intuition to the object .

Generalised metric

To motivate the definition of the generalised metric, observe the following. Suppose we have a Riemannian manifold . The metric is determined by its graph , where is the map given by . Then it can be found such that the restriction to the natural form to is positive definite.

Given the generalised tangent bundle for the smooth manifold , let the generalised metric be a positive definite subbundle of rank .

Given , define and , which is the orthogonal compliment of . We may now write with the form positive definite on and negative definition on . If we switch the sign on we can then obtain a positive definite metric on . Therefore, notice, a generalised metric can be explicitly viewed as equivalent to a reduction of the structure group of from to .

Crucially, note that as is isotropic, . So, similar to the standard Riemannian example, we can write as the graph where . We can now split into symmetric and anti-symmetric parts such that with

1. consisting of elements of the form ,

2. consisting of elements of the form .

It is then found that . Since is positive definite it follows is the standard metric in the Riemannian sense. So a generalised metric (note, we are only considering the untwisted case) is equivalently given by a Riemannian metric and a 2-form field . (From a string theory perspective, one’s intuition now obviously starts to indicate close connection to manifest T-duality invariance; we’ll get there soon).

Definition 1 Given that a generalised metric decomposes the generalised tangent bundle into positive and negative subbundles, another way to approach this idea is to define the bundle endomorphism defined as multiplication by . Then it can be shown that we have a bilinear form on that is symmetric and positive definite, and therefore a metric on the generalised tangent bundle .

If we now restrict to we obtain the Riemannian metric . Moreover, consider firstly the case . Then for a tangent vector , so that . Similarly , which means that in matrix form

But we of course restriction to standard Riemannian geometry is not interesting; we want to include the B-field. With the B-field switched on, where we define as the subbundles when . Intuitively, it can therefore be seen that where is (4). In matrix form, we explicitly find the generalised metric observed when studying the string spectrum under manifest T-duality invariance:

The B-field transforms with adjoint action, and a B-field transformation modifies linearly the B-field.

For the generalised metric, we find that it is therefore given by the matrix

with respect to which the norm of a generalised vector is then

with the metric on obtained by inverting .

Important to note, with the combination of the Riemannian metric and 2-form , we obtain the following parameterisation of the coset space

This statement is equivalent to the statement about the generalised metric defining a reduction of the structure group on from to . So at any point on the manifold, the space of such reductions is precisely the coset space given above. This means that there is a direct association between the NS-NS sector of the string and structure.

Under O(d,d) the generalised metric transforms as

We will make use of this wonderful identity on many occasions. Indeed, it resides at the heart of double field theory and the duality symmetric string. We will further more see that, from all that we have discussed so far, we will be able to define a new type of sigma model: namely, the double sigma model.

Generalised geometry #6: Dirac structures and subspaces

We’re almost at the point where we can start considering physics perspectives in relation to the mathematical structures of generalised geometry. But we still have some more definitions to review before arriving at such considerations. In this note, we consider Dirac structures.

As a gentle introduction, a Dirac structure is given by an orthogonal involution of whose eigenspaces do not see . The study of Dirac structures is a subfield of generalised geometry and relevant for the understanding of doubled geometry in a string theory setting. Generalised complex geometry is another subfield, summarised briefly at the end of this note, in which orthogonal complex structures on are studied instead of involutions. There are also other interesting structures on which involve neither Dirac structures nor generalized complex structures; however, we do not consider these.

Lie algebroids

There is an important remark to be made about subbundles, which will prove especially relevant in the analogous study of doubled geometry. The Frobenius integrability theorem [Sher11] connects the geometric concept of foliations with the analytic concept of involutive subbundles of the generalised tangent space. This raises the question of whether there exists a geometric interpretation of subbundles of which are involutive with respect to the Courant bracket. But more pertinently for these notes and our concern with the structure of doubled gauge transformations, we want to understand analogously the structure and properties of such subbundles of doubled spacetime.

Definition 1 (Lie algebroid) Let be a smooth manifold. A Lie algebroid is a vector bundle over equipped with the structures:

1. A bundle morphism called the anchor, or anchor map;

2. a bilinear form, typically a Lie bracket , on smooth sections satisfying a Lie algebra

such that is a Lie algebra homomorphism and the following relations are satisfied

where and .

Notice the second relation is a simplification of eqn. (19) in the note. Although not proven here, we’ll see that the relation {1) is true in the case of integrable maximal isotropics in which the Courant bracket satisfies the Jacobi identity on its sections.

Courant algebroids

Consider some candidate Lie algebroid, the bundle equipped with the Courant bracket has a natural choice for the anchor map, namely the projection . In this case, the first condition in (1) is satisfied because the Courant bracket reduces to the Lie bracket when restricted to sections of . But we don’t want to restrict to sections of , and for the second condition we also still have that the Jacobiator is non-zero. The moral is that for the generalised bundle we don’t have a Lie algebroid.

Instead, we should restrict to the subbundle , which is involutive (i.e., self-inverse is its own inverse) such that it is isotropic and closed under the Courant bracket. Then the inner products in the Nijenhuis operator vanish, meaning would be a Lie algebroid. It can also be proven now that the second condition is also satisfied.

Remark 1 (Motivating Courant algebroids) A lie algebroid can be given an intuitive description as simply the generalisation of a tangent bundle . We have built this picture from the ground up. As such, note that when projected (i.e., what is sometimes called “anchored”) to the tangent bundle , a Lie algebra is satisfied.

More on subbundles

Definition 2 (Courant integrable subbundles) Let be a subbundle of , then it is said is Courant integrable or Courant involutive if sections of are closed under the Courant bracket.

Remark 2 (Analogous to Frobenius integrable) This definition of a subbundle is analogous to the concept Frobenius integrable or Frobenius involutive for subbundles of that are involutive with respect to the Lie bracket.

Definition 3 (Maximal rank of subbundle) A subspace is isotropic if for all . Given that the inner product has signature , the maximal dimensions of the subspace is . In the case that the dimension of the subspace is , this is called a maximal isotropic subspace.

Remark 3 (Linear Dirac structures) In the literature, these subspaces are also sometimes referred to as almost Dirac structures. Given , if is involutive, then it is integrable and described as a Dirac structure. It is also possible to define a complex Dirac structure as the maximally involutive complex subbundle , which is an example of a complex Lie algebroid.

There are two types of Courant integrable subbundles. The first is of the type , where is a subbundle of and is Frobenius involutive. This example does not give any new types of geometry, and we don’t consider it any further. The second, most interesting type, are subbundles that are isotropic.

Further references

[Sher11] B. A. Sherwood. Frobenius Theorem [lecture notes]. url: http://www.math.uchicago.edu/~may/VIGRE/VIGRE2011/REUPapers/Sherwood.pdf.

Generalised geometry #5: Twisted by a gerbe

We can extend the theory of the generalised tangent bundle in two important ways:

1) Twisting by a gerbe,

2) Modifying the Courant bracket and exterior derivatives to twisted versions.

Twisting by a gerbe

In physics we think of a gerbe as a differential geometric object rather than an object of algebraic geometry. They can be seen as an analogue of fibre bundles, where the fibre is the classifying stack of a group. In differential geometry, gerbes give description to certain cohomology classes and the structures attached to them.

Definition 1 [Gerbe] In the context of generalised geometry, a gerbe should be considered as one of a number of objects in a hierarchy. Given a smooth manifold , the first object in the hierarchy that we may define is a function . Then, given an open cover of , we can also define a collection of functions such that on , we can say describing a 0-cocycle in . The next object in the hierarchy is a line bundle. This is simply a 1-cocycle . It follows that for some transition functions the third object in the hierarchy is a gerbe, which is a 2-cocycle in . This is a collection of valued functions defined on a triple intersection .

One then defines a connection on the gerbe as a collection of one-forms defined on the double intersections with . On triple intersections the connection satisfies

Taking the exterior derivative we get

Importantly, it can be proven that we can find 2-forms on the such that on double intersections

which leads to the globally defined 3-form

that in string theory is known as the Kalb-Ramond field flux. We may also think of this as the curvature of the gerbe.

Definition 2 [Twisting by a gerbe] Given a gerbe with connection the generalised tangent bundle may be twisted to produce a new vector bundle . Then, over each the fibres of are the same as ; but the transition from to the fibres are related by a B-transform

What we see, therefore, is that a section of is given by a collection such that on double intersections the relation is satisfied.

The bundle is called a twisted generalised tangent bundle.

There is a lot of additional structure that can be defined at this point, including a well-defined Clifford action and so on. But such discussion is excluded.

Twisted Courant bracket

Consider a gerbe with connection , we can then find 2-forms such that on the double intersection . These 2-forms yield an isomorphism which over is given by . Locally, the isomorphism is a B-transform. Define this B-transform by , then for sections and of we have

and

where over defines the curvature of the connection.

It is now the case that, identifying with , the bracket on the twisted generalised tangent bundle is not the Courant bracket but a modified version.

Definition 3 [Twisted Courant bracket] Let be a closed 3-form. On the sections and of , the twisted Courant bracket is given by

where it is required that is closed. The isomorphism now gives

with the twisted Courant bracket allows us to rewrite the two-form relation as

The twisted Courant bracket still satisfies all the conditions discussed in a previous note. However, it no longer satisfies the standard Lie bracket on vector fields due to the inclusion of an additional term. Its main advantage is that we may avoid using gerbes as we are only considering an untwisted generalised tangent bundle but with the extension of a twisted bracket. (Also requires a twisted exterior derivative on spinors, but we don’t consider this).

Generalised geometry #4: The Courant bracket and the Jacobiator

The Courant bracket

In addition to the generalised tangent bundle, the next fundamental structure of generalised geometry is the bilinear, skew-symmetric bracket called the Courant bracket.

The Courant bracket is defined on the sections of such that it is the generalised analogue of a standard Lie bracket for vector-fields on the tangent-space .

To begin, we may first start with a more general bracket: namely, the Dorfman bracket. Recall the following relations and standard definition for the Lie bracket,

Combining these two equations we find

which uniquely defines the Lie bracket. But in the same way vector fields have natural action of contraction on forms, there exists an extension of this action to generalised tangent vectors. This extension is given by Clifford multiplication. By replacing the contractions in (2) by the Clifford action of sections on we can then define a unique bracket operation on those sections of .

To determine this bracket we first look to the exterior derivative

Using this result then implies that, for the extension to the generalised bundle ,

This defines the Dorfman bracket.

Definition 1 (Dorfman bracket) Formally, the Dorfman bracket is defined on the sections . Its origin comes from the study of Dirac structures, taking the general form

which satisfies the Leibniz rule

for generalised vectors . The Dorfman bracket is closely related to the D-bracket in double field theory, and it can be used to define the generalised Lie derivative such that

Remark 2 (Lack of skew-symmetry and the Courant bracket) The Dorfman bracket is not skew-symmetric (this can be easily seen when calculating the generalised Lie derivative for some generalised tensor). In fact, as we’re about to discuss, its skew-symmetrisation is the Courant bracket.

Definition 3 (Courant bracket) The Courant bracket is a skew-symmetric, bilinear form defined for smooth sections on . It is given by

where denotes the usual Lie bracket of vector fields and denotes contraction with the vector field .

Note that the Courant bracket for vector fields reduces to the Lie bracket. The Lie derivative and the contraction satisfy the following relations:

Some properties of the Courant bracket

To study some properties of the Courant bracket, note firstly that from the Dorfman bracket we have the relation

which follows from the relation

What this shows is that if are orthogonal with respect to then . If we define the projection onto the first factor it follows

which, for the case of the Courant brackets, works out to be

Proposition 4 More generally, for sections of we have

Proof: Let , , and . Start with the right-hand side

Corollary 5 For sections of we have

such that, given the Dorfman bracket, if are sections and some arbitrary function we find

and, reversely,

It then follows more generally

Jacobi identity and the Jacobiator

Although the Courant bracket satisfies bilinearity and skewness; it does not actually define a Lie bracket on . This is because it fails to satisfy the Jacobi identity. To understand this failure let us first define the Jacobiator, which tells us in what way the Courant bracket fails to satisfy the Jacobi identity.

Definition 6 (Jacobiator) Define , then the Jacobiator can be written as

The Jacobiator is, in fact, the differential of the what is called the Nijenhuis operator. We won’t discuss this in detail here, but the main implication is that the Courant bracket generally satisfies the Jacobi identity up to some exact term.

Proposition 7 To better understand the Jacobiator, we can first look to the following identity for the Dorfman bracket (following lengthy derivation)

which says that acts as a derivative of the Dorfman bracket. If the Dorfman bracket was skew-symmetric, then this would be equivalent to the Jacobi identity.

Proof: Let , , and , then focusing on the right-hand side of (21)

Proposition 8 We can now also relate to such that

using the fact that when is a closed one-form.

With these relations, we can now calculate the Jacobiator.

Proposition 9 The Jacobiator defined above can be obtained as the differential of the Nijenhuis operator such that

where

which it should be noted is not tensorial in nature.

Proof:

And so, to end the proof, we see that we therefore have the structure of (24).

In the next entry, we’ll discuss gerbes and twisting before looking at the twisted Courant bracket.

Generalised geometry #3: Symmetries

When doing generalised linear algebra, we want to study transformations that preserve the canonical pairing from the last note (of signature ):

The group of linear transformations that preserve the inner product is the orthogonal group. What we’ll see is that the linear endomorphisms of preserving this bilinear form is the orthogonal group . The corresponding Lie algebra, which represents the algebra of infinitesimal transformations, is denoted by and, as we’ll see, . This is the Lie algebra of endomorphisms of which are skew adjoint with respect to the bilinear form.

Elements satisfy . Using the splitting of the direct sum we may write in matrix form

with , , , and . Note that these are all linear maps. So we find that the condition on R takes the form

For we have , which must hold for all . This implies , with the adjoint of (i.e., it is the pullback). Similarly, consider ; then . For the case , , it follows . It is from these conditions that satisfy (3) that we often read in the literature the Lie algebra consisting of matrices of the form

where, to be clear, is an arbitrary matrix generating . Now, for anyone who has studied some double field theory, all of this will start looking familiar. Moreover, note that B is a two-form such that generates what we call B-transformations. In the context of generalised geometry, are , with an element of . In the maths literature, and are noted as being skew such that

where the skewness implies alternativity.

Any endomorphisms of E that is skew adjoint with respect to the bilinear form can be viewed as a skew-symmetric bilinear form via . Under this identification we therefore have

Structure group generators

Let’s now look at the three primary orthogonal transformations belonging to . (What follows is a generalisation of the study of O(d,d) transformations on the level of the string spectrum. See, for instance, [Hitc10] and [Rub18]). The structure group reduces to generated by the following elements:

1. Diffeomorphisms: It is important that from (4), when we get for any the element

   

   where . Although the connection may not be immediately obvious, we will see in a much later discussion in what way this transformation relates to diffeomorphisms on the target space. For now, observe that its action on takes the form

   

   which yields a skew-symmetric action of on . Taking the exponential of (7) we get

   

   In the most general case for any we have an action

   

2. B-transformations: From (4) consider transformations parameterised by an anti-symmetric matrix with integer entries. The two-form corresponding to the orthogonal transformation

   

   acts as an endomorphisms of the generalised vector space such that

   

   and so its exponential then acts

   

   with the two-form having components . In the maths literature this B-transformation is also known as a shear transformation as it shifts but keeps V invariant. Similar to (7), the determinant of is +1.

   Remark 1 (Acting on generalised metric) The requirement that is anti-symmetric comes from the most general relations, which we first find in an analysis of the spectrum of the closed string. As we’ll see, we can define what is called a generalised metric (precisely the same as that in double field theory), which is a generalisation of the Riemannian metric that unifies and the 2-form in such a way that it is manifestly invariant under . When acting on the generalised metric, for the B-transformation we find

   

   In general, this correlates with a shift of the B-field not as a symmetry of the action but strictly as a duality transformation. In the case with a one-form on the worldsheet, these shifts are gauge transformations and they will be a topic of consideration in a later note.

3. -transformations: Similar to B-transformations, from (4) for these are transformations parametrised by an anti-symmetric matrix of the form

   

   The determinant of is also +1. It gives the following action on

   

   with its exponential

   

   where the action of the bi-vector field on forms is defined by way of contraction. So, for some one-form it follows with a local basis on the tangent space . This type of transformation shifts V and leaves invariant.

   Using and the elements we can write

   

   as

   

Patching and transition functions

Note that the non-trivial nature of the generalised tangent bundle discussed in Note #1 is encoded in transition functions between local patches .

Consider, moreover, the definition of a generalised vector also given in the same note. Given the generalised bundle , with and , we can write the generalised vector , in which denotes the sections on E, in component form

We discussed in the previous note linked above how this space comes equipped with an inner product and a metric. Let us now denote this metric as

It will become clear in a later note that satisfies all the requirements as an -invariant metric on the extended space (for the reader familiar with double field theory, this is indeed the constant metric we know well).

If we now introduce notation for the components of the generalised vector , using coordinate bases on and on over the patch , it is quite plain to see we can write as expected, where . For the index that runs over the entire extended space, it is conventional to use capital Latin letters . Hence,

Therefore, it is possible to define a basis

We’ll speak more of this metric later. Simply note for now that, as it is therefore possible to define a natural o(d,d) action on the generalised bundle E, it follows we can define a generalised structure bundle

which is a principle bundle with fibre that makes possible our previous discussion on the structure generators such that we were able to reduce the structure group to . The highest exterior power of E can be decomposed as

in which, given and , there exists a natural canonical pairing between both sides of this direct sum

It is conventional to make the identification so that the canonical orientation on E is defined by a real number.

Finally, returning to the discussion on patching, what this all means is that when studying the symmetries of this extended space we see that when transitioning from one patch to another , in principle diffeomorphisms should relate the vectors and the one-forms . So is non-trivial. Likewise, additional transformations of the one-forms encode the way in which is fibred over .

Remark 2 (T-folds and non-geometric backgrounds) In more advanced settings, such as when studying T-folds, we study transition functions that involve T-duality. In [Alf21], the global geometry of a T-fold is studied by dimensionally reducing a bundle gerbe on a torus bundle spacetime. Interestingly, it is then shown how the geometric structure underlying the T-fold can be interpreted as a particular case of a global tensor hierarchy. This is again something we’ll consider later, particularly in the context of double field theory.

More precisely, the transition between local patches and the diffeomorphism takes the form

where as the indices suggest, we are considering the overlap of two local patches .

As described in the previous section, if for now we interpret as an invertible matrix describing diffeomorphisms, a two-form, and denotes contraction with the vector field , then in component form for a generalised vector (27) can be expressed as

where the group is generated by elements denoted here as , . The two-form is typically restricted such that, in the case of a triple overlap, the one-forms must satisfy

As discussed more deeply later, this condition suggests that for the function , it is an element of given by . In the literature, this is interpreted to describe the structure of a gerbe, which at its most basic represents the analogue of a fibre bundle where the fibre is the classifying stack of a group. What it means is that geometrises diffeomorphisms and B-field gauge transformations [Alf21]. The role of gerbes in extended field theory and its geometry proves both interesting and important. It is a topic that is very much still in its infancy, with research in development.

What also becomes clear as one advances deeper in the study of generalised geometry, is that there is a natural correspondence between the patching 1-forms and the B-transformation. Indeed, as will become clear, the role of this B-transformation is no coincidence and, from view of string theory, we see that corresponds directly to the 2-form NS-NS potential. So already, and certainly as we progress in these notes, we’re starting to see some very nice features that given an interesting geometric perspective on the target space of the string. Acting as a generator of the subgroup , we will learn explicitly how the overall structure group is necessarily given by the semi-direct product and embeds as a subgroup of . This structure is actually quite interesting from the perspective of double field theory, but there is still much more to uncover before such considerations.

References

[Alf21] L. Alfonsi. Doubled Geometry of Double Field Theory [PhD thesis]. url: https://researchprofiles.herts.ac.uk/portal/files/26014618/2108.10297v1.pdf. [Gual04] M. Gualtieri. Generalized complex geometry [PhD thesis]. arXiv: 0401221[math.DG]. [Hitc10] N. Hitchin. Lectures on generalized geometry. arXiv: 1008.0973 [math.DG]. [Rub18] R. Rubio. Generalised geometry: An introduction [lecture notes]. url: https://mat.uab.cat/~rubio/gengeo/Rubio-GenGeo.pdf

Generalised geometry #2: Generalised vector space and bilinear form

Generalised linear algebra

In the first note we introduced one of the fundamental structures of generalised geometry, namely the generalised tangent bundle . In the extension of the standard tangent bundle to , we are simultaneously extending linear algebra to some notion of generalised linear algebra. This is a point nicely emphasised in Roberto Rubio’s lecture notes.

Think of it this way. In standard differential geometry we have the tangent bundle , whose sections are endowed with a Lie bracket satisfying the Leibniz rule

In generalised geometry, on the other hand, we are motivated to extend linear algebra to generalised linear algebra such that we replace the standard vector space of differential geometry with the generalised vector space

with a d-dimensional vector space and its dual. We can denote the elements of this space with and .

For intuition, realise that this extension can be motivated at its most basic when studying symplectic forms that represent a skew-symmetric analogue of an inner product: i.e., skew-symmetric isomorphisms or . This also takes us into a study of linear presymplectic and Poisson structures, but such preliminary discussion is dropped in these notes.

Definition 1 (Canonical pairing and inner product signature) Given the generalised vector space , then for two generalised tangent vectors there exists a canonical metric naturally equipped on this space such that

which is a maximally indefinite inner product of signature . Note that denotes contraction by . The factor of is purely convention with no geometric meaning.

Next, define a subspace . Then the orthogonal compliment for this pairing can be defined in the standard sense

It is said that is isotropic if . The idea of maximally isotropic subspaces raises interesting considerations, particularly globally defined structures with an integrability condition, which are often studied under the heading of linear Dirac structures. As a matter of introduction, if is isotropic but not constrained in an isotropic subspace than it is maximally isotropic.

The bilinear form (3) can be verified by taking a basis for with dual basis for . Then we can define as the total basis for , wherein the inner product admits a diagonal form .

Explicitly, consider the basis with the canonical pairing given by

in which the signature is with an orthogonal basis of vectors of positive length and vectors of negative length. It can then be shown that the dimension of the maximally isotropic subspace must be at most . In fact, this statement is true for any maximally isotropic subspace.

Proposition 2 For a vector space , we have that is the dimension of any maximally isotropic subspace of .

Proof: Let be a maximally isotropic subspace. Consider to be semidefinite such that or for all . Otherwise, consider a compliment so that , then if contains two vectors with and , a suitable linear combination would be null. As a result would be isotropic containing . Additionally, as we have

On the other hand, given that the pairing is non-degenerate, we write such that we now have

which is to say so .

What we have found is that, as is a vector space of dimension with a symmetric pairing of signature , there is a choice two maximally isotropic subspaces.

Remark 1 (Motivation) There is another way to motivate the inner product (3) by simply noting that and are vector spaces, and, as they are related by a duality transformation (this will be made clear later) we obtain a natural bilinear symmetric form.

Brief remark: Clifford E modules

The bilinear form (3), or what is also referred to as the canonical metric or canonical pairing, should not be confused with a metric in the standard sense. To obtain an ordinary metric, we must introduce extra structure.

To make sense of this claim, consider the generalised bundle from note 1 [LINK]. Each fibre of has an action on the corresponding fibre of the exterior bundle given by

It follows that

which gives description of the exterior algebra in terms of the structure of a bundle of Clifford modules with respect to the natural bilinear on . Typically, in the literature the corresponding Clifford algebras generated by is denoted Cliff(E).

To conclude: as we’ll see, the form on enables the reduction of the structure group of to . In fact, in the maths literature we see that further reduction to the structure is possible. This will be the topic of the next note, as we focus on symmetries and the structure group generators.

Generalised geometry #1: Generalised tangent bundle

1. Introduction

The motivation for generalised geometry as first formulated in [Hitc03], [Hitc05], and [Gual04] was to combine complex and symplectic manifolds into a single, common framework. In the sense of Hitchin’s formulation, which follows Courant and Dorfman, generalised geometry has deep application in physics since emphasis is placed on adapting description of the physical motion of extended objects (i.e., strings). In this way, one can view generalised geometry as analogous to how traditional geometry is adapted to the physical motion of point-particles. There are also more general forms of generalised geometries, which can be thought of as further extended and adapted geometries to describe higher dimensional objects such as membranes (and hence also M-theory). These notions of geometry, which we can organise under the conceptual umbrella of extended geometries, correlate closely with the study of extended field theories that captures both Double Field Theory (DFT) and Exceptional Field Theory (EFT).

In these notes, interest in generalised geometry begins with the way in which generalised and extended geometry makes manifest hidden symmetries in string / M-theory. In particular, emphasis is on obtaining a deeper understanding and sense of mathematical intuition for the structure of generalised diffeomorphisms and gauge symmetries. The purpose was to then extend this emphasis to a study of the gauge structure of DFT, which is well known to be closely related with generalised geometry but in fact extends beyond it. We won’t get into this last concern in these notes; it is merely stated to make clear the original motivation for reviewing the topics.

Given that generalised geometry inspired the seminal formulations of DFT, it is no coincidence that what we observe in a detailed review of generalised geometry is the way in which the metric and p-form potentials are explicitly combined into a single object that acts on an enlarged space. This enables a description of diffeomorphisms and gauge transformations of the graviton and Kalb-Ramond B-field in a combined way. In fact, one of Hitchin’s motivations for the introduction of generalised geometry was to give a natural geometric meaning to the B-field. As will become clear in a later note, a key observation in this regard is that the automorphism group of the Courant algebroid is the semidirect product of the group of diffeomorphisms and B-field transformations. We will then study the structure of this group.

Remark 1 (Generalised geometry, branes, and SUGRA) Although not a focus of these notes, it is worth mentioning that generalised geometry in the sense of Hitchin is an important framework for studying branes and also T-dualities, including mirror symmetry. It also offers a powerful collection of tools to study Calabi-Yau manifolds, particularly generalised Calabi-Yau, proving important in the search for more realistic flux compactifications.

2. Generalised tangent bundle

The main objects to study on generalised geometry are Courant algebroids. But before we reach this stage, there are two fundamental structures of generalised geometry that we must first define: 1) the generalised tangent bundle and, 2) the Courant bracket. In this note, we introduce the generalised tangent bundle. Then in the following notes we explore the properties of this structure and the related extension of linear algebra to generalised linear algebra. This brings us to finally study the Courant bracket, its properties and symmetries, before we study Courant algebroids and generalised diffeomorphisms.

Definition 1 (Generalised bundle) The generalised tangent bundle is obtained by replacing the standard tangent bundle of a D-dimensional manifold with the following generalised analogue

The generalised tangent bundle is therefore a direct sum of the tangent bundle and co-tangent bundle . As we will learn, the bundle has a natural symmetric form with respect to which both and are maximally isotropic.

Remark 2 (Notation) Often in these notes we will use and interchangeably, which should be clear in the given context.

The generalised bundle (1) fits the following exact short sequence

which, later on, we’ll see is the sort of sequence that describes an exact Courant algebroid.

Remark 3 (Early comment on Courant algebroids) As we will study in a later entry, it is the view afforded by generalised geometry that the bundle is in fact an extension of by , and so it is a direct example of a Courant algebroid such that, in the exact sequence (2), the Courant algebroid has a symmetric form plus other structure (e.g., the Courant bracket) that makes it isomorphic to . This is true for suitable isotropic splittings of the exact sequence, an example of which is called a Dirac structure.

The sections of are non-trivial sections of . This means that, unlike in standard geometry and how we typically consider vector fields as sections of only, we now consider elements of the non-trivial sections

where are vector parts and 1-form parts.

The set of smooth sections of the bundle are denoted by such that the set of smooth vector fields is denoted by and the set of smooth 1-forms by .

Remark 4 (Sequence and string background fields) For the sequence (2), note that in the map there exist sections that are given by rank 2 tensors, which can then be split into symmetric and antisymmetric parts, . The sections of describe infinitesimal symmetries of these fields, as they are encoded in a generalised vector field capturing infinitesimal diffeomorphisms and a 1-form describing the b-field gauge symmetry.

References

[Gual04] M. Gualtieri. Generalized complex geometry [PhD thesis]. arXiv: 0401221[math.DG]. [Gua11] Marco Gualtieri. Generalized complex geometry. Ann. of Math. (2), 174(1):75–123, 2011. url: https://annals.math.princeton.edu/wp-content/uploads/annals-v174-n1-p03-s.pdf. [Hitc03] N. Hitchin. Generalized Calabi–Yau manifolds, Quart. J. Math. Oxford Ser. 54 (2003) 281. arXiv: 0209099 [math.DG]. [Hitc05] N. Hitchin. Brackets, forms and invariant functionals. arXiv: 0508618 [math.DG]. [Hitc10] N. Hitchin. Lectures on generalized geometry. arXiv: 1008.0973 [math.DG]. [Rub18] R. Rubio. Generalised geometry: An introduction [lecture notes]. url: https://mat.uab.cat/~rubio/gengeo/Rubio-GenGeo.pdf

(n-1)-thoughts, n=6: Asperger’s and writing, Lie 2-algebroids, linguistics, and summer reading

Asperger’s, studying, and writing

As a person with autistic spectrum disorder (ASD), I’ve learned that writing plays an important and meaningful role in my life. I write a lot. By ‘a lot’ I mean to define it as a daily activity. Sometimes I will spend my entire morning and afternoon writing. Other times I will be up through night because my urge to write about something has kept me from sleeping. Most often I write about maths and physics, keeping track of my thoughts and ideas, planning essays, or writing about my work. But I also make it a principle of life to read widely. Indeed, I enjoy reading – studying – as much as I enjoy writing, and this often motivates me to write about many other topics. The two go hand-in-hand.

One reason writing has become important for me has to do with how, as a person with Asperger’s, social communication (by which I mean verbal, but of course also entails other forms like sign) is a source of struggle. I don’t often write about my Asperger’s, mainly because I find it a difficult process. It is hard to organise my thoughts about it, and I am never sure what is appropriate to share. In formal language, my Asperger’s is described clinically as high-functioning but severe. A big part of my life is about learning new strategies to cope. Some of the strategies may even be familiar to others without ASD, like learning to talk in front of others in ways that minimise anxiety and stress, or without completely freaking out (what we call in my language ‘red card’ moments). Or, to give another example, we work on finding strategies for the times I am at the office, so my brain doesn’t go into hyperdrive and so I can focus on discussion and also things like writing on the whiteboard. Another thing about my Asperger’s is that it can be hard adjusting to new people and it can be very stressful acclimatising to new environments. I’ve been working with Tony, now my PhD supervisor, for two years or more and I have only recently started to acclimatise and find our engagement a bit easier to manage. Indeed, in the same time I’ve been at the University of Nottingham, it remains an ongoing process adjusting to this new environment and to being on campus. Like with my close friend, Arnold, who, even after seeing him everyday for years, it was often still a challenge for me to engage with him socially and to visit his house. There is a lot to my experience, not just the social aspect of experience, that can be difficult and demanding as well as overwhelming. I also struggle a lot with anxiety and other things, in addition to extreme sensory sensitivity. So I require a lot of time and space for stillness in my own environment, with my own structure and routine – usually in my own space with my books and other comforts – because sensory overload can easily overwhelm.

In my one attempt to write about living with ASD I expressed how it can be difficult to understand cultural meanings as another example. This is a way of describing orientation to many of the ‘codes’ or behavioural routines that normalise in society. For example, I remember when I was a teenager being pressured a lot to establish the same routine economic patterns as others, or blamed because I didn’t have a job or couldn’t maintain one. I find it difficult to compute things like why daily life is the way it is for most individuals or why people behave as they do. What motivates daily behaviour and routine? How do people make decisions or direct the future course of their lives? Science, textbooks, and studying fervently became, at least in part, a survival-based mechanism. There is no instruction manual about humans; or about why history has taken the path it has in the course of human and societal development; or why many arbitrary social customs have come to be the way they are; or why my father acted and behaved the way he did; among many other things that come to be a feature of life. Studying became my way to cope and to understand, and writing became an extension of that. For instance, I studied every aspect of psychology to help better understand my experiences growing up or why, at least in part, people act violently or use violent language. I’ve read and written across most of philosophy; the same for economics, certainly enough to understand the fundamental debates; and also a lot of sociology. At one point I read a lot of political history, with history one of my favourite subjects. While all of this has a purpose in aiding my attempt to try and understand the world I am a part of, it also supports my passion for studying, my focused interests, and provides the stimulation I need.

On top of it all, living with Asperger’s can be quite exhausting. Indeed, one thing that is common for people diagnosed with autism is the experience of a certain type of fatigue, or what, in my house, we call ‘crashes’. These are a daily experience, where I need to put on my headphones and sit in my own (still and comfortable) space for however long it takes to calm my brain. For these reasons, day to day life is often spent in controlled environments, because it helps ease the red card moments, reducing stress and anxiety, and thus also helps combat the amount of crashes.

I think it all adds up in some sort of complicated sum as to why I find writing an important outlet. But even writing has its own difficulties. I remember my teacher, when I was 6 or 7 years old, say that my brain runs faster than my pen. I think this is true. I think of the sluggish pen effect as the difficulty in converting the internal representations of whatever concept or idea into concise written form at the pace I wish to feed ink to paper. So even though I write everyday and have been practising for many years, the usual result of my writing is typically permeated with errors. The process can be disabling and discouraging, to be honest, with many moments of frustration and failure; but, I’ve also learned that when I battle through and produce something I am happy with, the moment of victory is worth so much.

For many personal reasons, I’ve been regularly encouraged to write more and share more on my blog, and this is something I’ve been working toward. I think that, over a couple of years, I’ve grown more and more comfortable sharing essays and technical notes, although perhaps that is especially true in recent months; but I am also practising writing in other ways, like more personally and less formally. Technical writing is much easier than informal discussion, although a definition of the latter still seems somewhat unclear.

So as one step, this is a new blog post format that I may start experimenting with over the coming weeks, in addition to my usual research entries, essays, and technical notes. Although I prefer to keep my blog focused on my maths and physics research, which of course is mainly string related, allowing from time to time the inclusion of the odd bit of academic diversion, I think this (weekly or fortnightly) format of (n-1)-thoughts may be a fun space that allows me to practice writing in different ways, to share disconnected thoughts or random interests, outside of the formal essay or technical structure.

Generalised geometry, higher structures, and some John Baez papers

Another gem by, Urs! In a recent post on higher structures and M-theory, I made a comment recommending that people read Urs Schreiber’s many notes over the years. In my own research, I’ve found them to be invaluable. The most recent example relates, in some ways, to what I also mentioned in that post about how we may motivate the study of higher structures in fundamental physics: namely, how the Kalb-Ramond 2-form can be seen as an example of a higher structure as it is generalised from the gauge potential 1-form. I won’t go into details here, but the other day I was thinking about such generalisations, and I was thinking about Hamiltonian mechanics in the process. As I’ve mentioned before, if I were to teach string theory one day I would take this approach, emphasising at the outset the important generalisation from point particle theory to the extended object of the string.

Thinking of higher structures, I knew there were many connections here, and I was wanting to fill out my notes, for instance from how in generalised geometry the algebraic structure on is a Courant Lie 2-algebroid. Those who study DFT will likely be quite familiar with Courant algebroids, and, certainly from a higher structure perspective this line of study is interesting. I also knew there was an original paper, which I had seen in passing, talking about this and the relation to symplectic manifolds, but I couldn’t find it. Then, bam! As Schreiber notes in a forum reply, ‘Courant Lie 2-algebroids (standard or non-standard) play a role in various guises in 2-dimensional QFT, thanks to the fact that they are in a precise sense the next higher analogue of symplectic manifolds and thus the direct generalization of Hamiltonian mechanics from point particles to strings’.

The part ‘from point particles to strings’ was hyperlinked to an important paper, the very paper I was looking for! The paper is Categorified Symplectic Geometry and the Classical String by John C. Baez, Alexander E. Hoffnung, Christopher L. Rogers. I look forward to working through this.

I also want to highlight several other papers from around the same time by Baez, including one co-authored with Schreiber, that I think are also foundational to the programme:

Categorification co-authored with James Dolan;

Higher-Dimensional Algebra VI: Lie 2-Algebras co-authored with Alissa S. Crans;

Lectures on n-Categories and Cohomology co-authored with Michael Shulman;

and, finally, Higher Gauge Theory co-authored with Urs Schreiber.

Thinking about my summer reading list

My summer holiday is in June this year, as I have a conference in mid-July and then I am scheduled to return back to university 1 August. I think Beth and I are going to spend a week in a North Norfolk, one of our favourite places, which has also sort of become a home for both of us. In anticipation of my break, I’ve started putting together my summer reading list, as I do every year. To be honest, there are so many good books right now, it is difficult to choose.

Although my list isn’t complete, one book that I’m already looking forward to is Jennifer Ackerman’s ‘The Genius of Birds‘. I had this book on my Christmas break reading list but, unfortunately, I didn’t have enough time to get to it.

I recently purchased ‘Explaining Humans: What Science Can Teach Us About Life, Love and Relationships’ by Camilla Pang, and I think I will add this to my list. Camilla has a PhD in biochemistry and, as she also has ASD, my interest in this book is more so about her personal journey coming to grips with the complex world social around her through the lens of science. It sounds, on quick glance, that we’ve come to cope with the world in similar ways and share an interest in understanding human behaviour and development. Having said that, I think there is a bit of a risk that people might read this book and conflate it with some sort of autistic worldview, which is completely incorrect, or, equally incorrect, as a scientific view of human behaviour. Contrary to some reviews, I wouldn’t read Pang’s book looking for a strictly scientific view (else one will be disappointed). I could be wrong, but I think ‘Explaining Humans’ may have potentially been mispromoted, hence some of the confused feedback. I approach this book as I would when reading someone’s memoirs, like ‘Diary of a Young Naturalist‘ by Dara McAnulty, ‘Lab girl‘ by Hope Jahren, or ‘Letters to a Young Scientist‘ by Edward O. Wilson. With topics including the challenges of relationships, learning from mistakes, and navigating the human social world by finding tools in things like game theory and machine learning, my interest is in the fact that this is another author with autism and, for myself, I similarly use textbooks and my studies to understand and manage my experience the world. Even on a purely phenomenological level, it will be interesting.

Another book that I may add is of a completely different tone: namely, Saul David’s ‘Crucible of Hell’. I’ve been enjoying reading about WWII again, and, as noted in this post on Dan Carlin’s podcast series on the events in the Asiatic-Pacific theatre, the battle of Okinawa (and others) I haven’t read much about. A few more books I have been thinking about: Douglas R. Hofstadter’s ‘Gödel, Escher, Bach: an Eternal Golden Braid‘, ‘The Deeper Genome‘ by John Parrington, ‘King of Infinite Space: Donald Coxeter, the Man Who Saved Geometry‘ by Siobhan Roberts, ‘Decoding Schopenhauer’s Metaphysics’ by Bernardo Kastrup, ‘Quantum Computing Since Democritus‘ by Scott Aaronson, Jared Diamond’s ‘Guns, Germs, and Steel: The Fates of Human Society‘, and Daniel Kahneman’s latest ‘Noise: A Flaw in Human Judgement‘. Tough decisions.

Linguistics

I’ve been short on time this week finishing some calculations and working on a paper, prior to receiving my second Covid jab. But the other afternoon I thoroughly enjoyed this article. It’s on the Galilean challenge and its reformulation, wherein discussion unfolds on why there is an emerging distinction between the internalised system of knowledge and the processes that access it.

As alluded a moment ago, a general theory of development has interested me for a long time. For my book published by Springer Nature, a lot of the study and references were originally motivated by this interest. When I last did an extensive read on the topic, there was a lot of progress in developmental models – biology, bio- and neuro-linguistics, child psychology, and so on. The summer when I was writing my book, I had already compiled all of my research and I was running short on time in terms of the writing process (I wrote the book in the span of two weeks). Around the time of my research, if I recall there was discussion in biolinguistics regarding the hypothesis of ‘[t]he fibre tract [as one reason] for the difference in language ability in adults compared to pre-linguistic infants’. I remember noting that interesting ideas were developing, and this is a nice article on that front. What is particularly fascinating, I would say, is how language design appears to maximise computation efficiency, but ‘disregards communicative efficiency‘ [italics mine].

This certainly runs directly counter to common belief, as mentioned in the article, namely the established view that communication is a basic function of language. For a long time, as I understand it, there was belief that there was an experiential component to early language formation; but what current research suggests is that, an experiential component is not fundamental at all. Of course an experiential component plays a role, in some capacity, when it comes to externalisation processes, such as in development of variances in regional accent here in England as an example. I mean, the subject is mediated (to whatever degree) by his/her sociohistorical-cultural circumstances, but, unless I am misunderstanding (I need to read through the research more deeply) language itself is not some purely social construct.

Regarding reference to the evolutionary record, I wonder how the developing view in the article relates to ongoing research concerning, for example, certain species of birds, their migratory paths, and the question of inherited or genetic knowledge. It’s an absolutely fascinating area of study, something I’ve been reading about with my interests in mathematical biology, and of course there is very apt analogy here also with broader developments in microbiology.

One last thing of note from reading the article, as I have written quite a bit about the enlightenment philosophes and the start of modern science, it is notable how they sought to ask the question of language. Descartes’ fundamental enquiry into language – the Cartesian question – remains interesting to this day, and I was delighted to see it referenced at the outset. I recommend reading Descartes’ meditations plus other contributions to the enlightenment philosophes – Kant, Spinoza, Hume, to name a few. There is so much here that remains relevant to our modern history and to the development of the contemporary social world. For a few years I’ve been writing a series of essays on Hegel’s science of logic and his epistemology, which is notably relevant today in my area of work in fundamental maths/physics.

Mental health awareness week

Finally, it’s mental health awareness week in the UK. Often these sort of campaigns can be incredibly superficial, failing to look at root causes or ask fundamental questions about well-being and support, but they don’t have to be. Mental health awareness is something that I’ve always taken seriously, not least because I have experienced many challenges with my own mental health throughout my life. The last time I did research and wrote on the subject, suicide statistics in many leading Western countries were significant. I know, too, that for people with autism, like myself, mental health can present a significant challenge in addition to the other challenges one may face. People with autism are much more likely to die by suicide than the general population, as many cause-specific analyses of mortality for people with autistic spectrum disorder (ASD) indicate. Sometimes these facts are overlooked when we talk about mental health as a society, and often I find it important to highlight. But mental health doesn’t discriminate, it affects all people from all backgrounds, and weeks like this one are a good time to help foster discussion, combat stigma, and to think about mental health in all of its facets.

*Image: ‘Streams of Paint‘ by markchadwickart (CC BY-NC-ND 2.0).